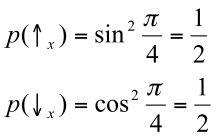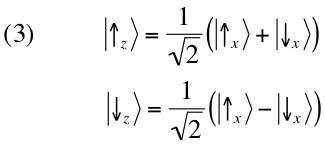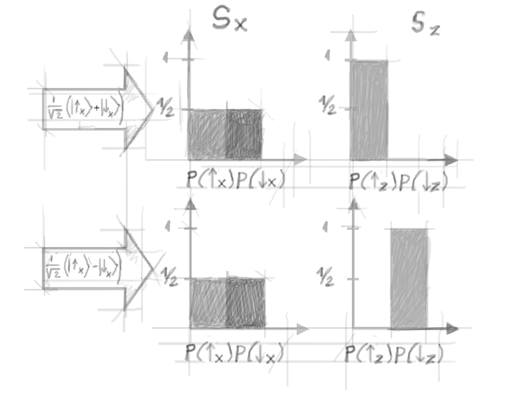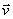
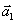
SOBREPOSIÇÕES > Origens Os estados quânticos podem ser representados por vetores pertencentes ao chamado Espaço de Hilbert. Os vetores fornecem a estrutura ideal para representar regularidades específicas, especialmente quando observáveis incompatíveis estão envolvidas. 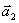Para ver como isso funciona, seja um vetor de comprimento unitário no plano e considere suas projeções em dois eixos ortogonais e (figura 5). Pelo teorema de Pitágoras:



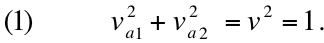
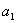
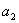
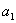
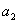
Agora suponha que nós medimos um observável A que somente pode assumir dois valores, e . As probabilidades de obter e variam em função da forma na qual o sistema medido tenha sido preparado.

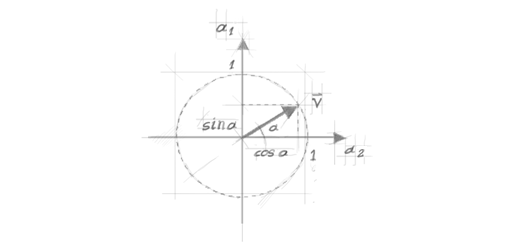
Figura 5. Um vetor unitário no plano e suas projeções no eixo.

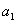
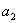
Ainda assim, desde que e representem resultados mutuamente excludentes que esgotam o espectro de ocorrências possíveis, nós sabemos a priori que, em todos os casos, as probabilidade correspondente obedece à condição:



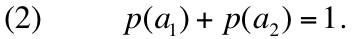
O formalismo preditivo da teoria quântica é baseado no paralelismo entre a eq. (1) e a (2). Ele é resumido pelas seguintes regras:

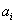
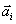
I. Os valores que um observável A pode assumir são representados por eixos ortogonais gerando um espaço de estados.

II. Cada procedimento experimental que ‘prepara’ um sistema antes de uma medição de A é representado por um vetor de estado 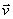pertencente ao espaço de estados e tendo comprimento unitário.

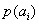
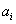
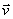
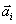
III. (Regra de Born) Se nós medirmos o observável A, a probabilidade de obter o valor é dada pela módulo quadrado da projeção de sobre o eixo:

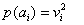
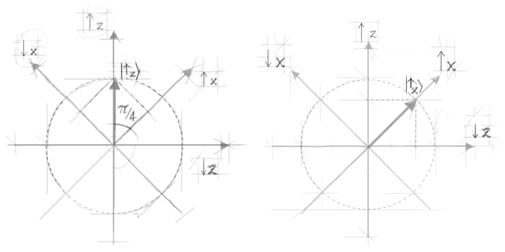
Figura 6a e b. Representação do autovetor 'para cima' de Sz . O vetor antiparalelo serviria tão bem quanto esse - nós escolhemos arbitrariamente vetores pertencentes ao semicírculo unitário positivo para representar os estados quânticos.

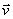
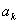
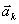
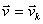
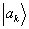
Um corolário importante das regras I-III é o seguinte: o vetor de estado que corresponde ao caso especial no qual nós prevemos com absoluta certeza (i.e. com probabilidade 1) que a medição de A terá como resultado o valor é o vetor unitário que está no eixo ( ). Usando a notação de Dirac, esse vetor é descrito por e chamado de um autoestado (ou autovetor) de A.

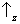
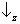
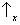
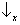
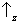
Vamos aplicar as mesmas regras simples aos experimentos de Stern-Gerlach discutidos na seção sobre evidência experimental. Nós estamos focados em dois observáveis de spin: S_z, que pode assumir os dois ‘valores’ e ; e S_x, que pode assumir os dois ‘valores’ e . No primeiro passo do experimento (figura 2) somente aqueles átomos para os quais uma medição de S_z tem como resultado são selecionados. 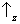Para esses átomos, nós encontraremos com certeza se uma medição de S_z for repetida. 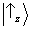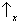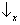Assim, o vetor de estado associado é .Se, sobre a amostra de átomos assim preparada, nós agora medirmos S_x, nós encontraremos para metade dos átomos e para a outra metade (passo 2 da figura 3). Esse resultado pode ser representado no nosso espaço de estados? 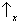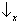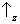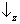Sim, é suficiente tomar os dois eixos correspondentes a e (ver regra I) formando um ângulo de π/4 com os eixos correspondentes a e (figura 6a). 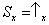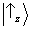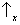De acordo com a regra III, para conseguir descobrir a probabilidade de encontrar nós temos que projetar o vetor de estado sobre o eixo correspondente a (figura 6a). Da mesma forma nós calculamos a probabilidade de que a medição de S_x vai ter como resultado . 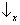Nós obtemos:



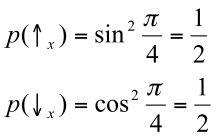
O resultado do terceiro experimento (figura 3) pode ser formalizada de modo direto da mesma forma, observando que os dois primeiros aparatos ‘preparam’ o estado 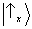(figura 6b).

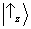
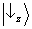
Vamos ver como os fenômenos de interferência são levados em consideração neste modelo simples. Manipulando as regras básicas da composição de vetores no plano, os vetores e podem ser reescritos como:



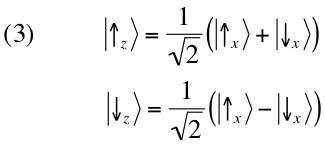
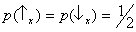
Note que ambos esses estados preveem a mesma distribuição de probabilidade para uma medição de S_x: . Assim, os dois estados (ou, para ser mais preciso, as preparações correspondentes) não podem ser distinguidas a posteriori pela realização de tal medição. As duas preparações, entretanto, fornecem resultados estatísticos opostos se uma medição de S_z for realizada (figura 7). 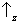No primeiro caso, sempre se encontrará ‘ ’; enquanto que no último, isso nunca acontece. Esse ‘nunca’ é a assinatura da interferência (compara com as franjas claras e escuras do experimento de dupla-fenda). Note que a única diferença matemática entre os dois estados(3) é o sinal da sobreposição: positivo no primeiro caso, negativo no segundo. 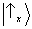Esse sinal expressa a relação de fase existente entre e . 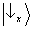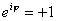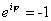(Usando notação complexa, ou dependendo se φ = 0 ou φ = π; vale a pena comparar com o caso das ondas.)

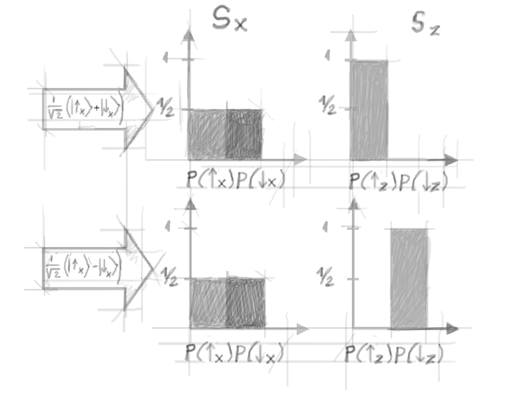
Figura 7. Comparação das distribuições de probabilidade previstas por duas sobreposições diferentes de autoestados de Sx'.

Até agora, nós estávamos nos preocupando com uma classe especial de observáveis, aqueles que podem ser representados por eixos ortogonais diferentes dentro do mesmo espaço de estados. As distribuições de probabilidade associadas com tais observáveis são rigidamente conectadas entre si. No caso de S_z e S_x, por exemplo, nós vimos que, dada uma distribuição equiprovável de ‘para cima’ e ‘para baixo’ para S_x, a estatística de S_z segue necessariamente uma das duas distribuições representadas na figura 7.

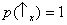
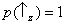
Entretanto, existem observáveis cujas respectivas distribuições de probabilidade são a priori completamente independentes. Um exemplo típico é o dos observáveis de spin de duas partículas distintas. A partícula 1 pode ser preparada de tal forma que e a partícula 2 de tal forma que . (Isto não pode ser feito se S_x e S_z forem medidos na mesma partícula, já que S_x e S_z são observáveis incompatíveis.) Em geral, entretanto, uma vez que dois sistemas quânticos tenham interagido, eles se tornam correlacionados de modo que os resultados de medidas não podem ser mais previstos simplesmente se atribuindo um vetor de estado individual para cada sistema parceiro. Ao invés disso, um vetor de estado único e global deve ser associado com todo o par. Esse estado é construindo ao se combinar os vetores de estado individuais, mas pertence a um espaço de estados mais amplo. Um estado emaranhado de duas partículas de spin ½ é o seguinte:



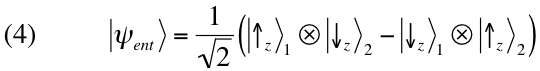
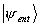
As previsões estatísticas associadas com o são muito importantes. A probabilidade de encontrar ‘para cima’ ou ‘para baixo’ se S_z (ou qualquer outra componente de spin) for medida em cada partícula separadamente é 1/2. Além disso, se uma das partículas for encontrada com spin ‘para cima’ na direção z, o resultado de qualquer medição de spin realizada subsequentemente na outra partícula seguirá as estatísticas previstas por . 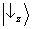Se, ao contrário, a primeira partícula for encontrada com spin ‘para baixo’ na direção z, então as estatísticas da outra partícula serão aquelas correspondentes a . 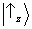Devido a forma peculiar do estado (4), correlações análogas existem para qualquer componente de spin. 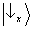Assim, se, por exemplo, a partícula 1 for encontrada com spin ‘para cima’ na direção x, a partícula 2 seguirá as previsões de ; e assim por diante (a situação está representada na figura 4). 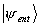De fato, preserva sua forma matemática se expresso em termos dos autovetores de S_x:

.

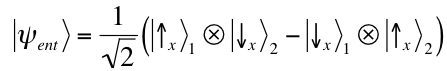
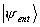
As distribuições de probabilidade observadas em medições realizadas em uma partícula individual são fundamentalmente diferentes dependendo se a partícula tem ou não um par emaranhado. No primeiro caso, como mostrado na figura 8, os efeitos de interferência são eliminados (isso pode ser facilmente derivado da definição acima de usando as fórmulas (3); ver também complementaridade).

No modelo simples utilizado em nossa apresentação, o espaço de estados era o plano real da geometria euclidiana e os resultados eram representados pelos eixos. Entretanto, uma análise completa de todas as medições possíveis em um Stern-Gerlach mostra que este espaço é insuficiente para fornecer uma representação completa. Uma estrutura geométrica mais rica, o espaço de Hilbert, definida no campo dos números complexos, deve ser introduzida. Dentro desta estrutura, os resultados são representados por subespaços, e os observáveis por combinações de projetores sobre esses subespaços.

Figura 8. Distribuições de probabilidade encontradas quando a partícula testada (partícula 1) tem uma parceira emaranhada.