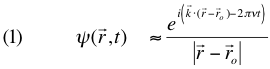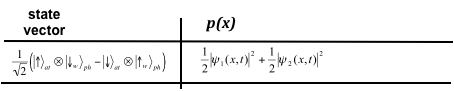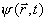
, chamado de amplitude de probabilidade, a um ponto qualquer 
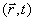
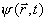
no espaço e no tempo. contém parte da informação codificada no estado quântico do sistema,
e permite calcular a probabilidade dos possíveis resultados das medições envolvendo variáveis cinemáticas tais como posição e momentum. O quadrado do módulo da função de onda, 
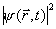
, fornece, por exemplo, a probabilidade de encontrar o sistema em 
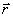
um tempo t (esse resultado importante pode ser derivado da regra de Born). De acordo com as relações de de Broglie, a função de onda associada com o feixe de partículas, todas com momentum p e energia E, é uma onda monocromática de comprimento de onda λ = h/p e frequência ν = E/h . Por exemplo, uma onda esférica fornece uma boa aproximação para a função de onda associada a uma partícula propagando-se a partir de uma fonte pontual:
(
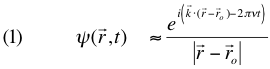
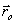
sendo a posição da fonte, 
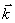
sendo o vetor de onda regendo a propagação da onda, cujo módulo é 2π/λ). Note que, neste exemplo, 
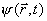
difere significativamente de zero ao longo de uma grande região do espaço. Isso significa que a distribuição que descreve a probabilidade de detectar a partícula em uma dada posição não é localizada
. Sistemas bem localizados (i.e.
objetos corpusculares) não são associados a uma onda monocromática, mas sim com um pacote de onda. Pacotes de onda podem ser considerados como sobreposições de um número infinito de ondas monocromáticas de diferentes comprimentos de onda, interferindo destrutivamente em todos os lugares menos em uma pequena região na qual elas somam construtivamente dando origem a um sinal. As extensões espectrais e espaciais de um pacote de onda devem obedecer às relações de incerteza. O padrão de interferência observado no experimento da dupla-fenda é facilmente compreendido em termos da função de onda. As duas fendas dividem a onda associada com o feixe de átomos incidente em duas ondas esféricas secundárias
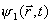
e 
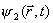
(como na figura 3). A função de onda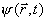 
do átomo após o filtro da dupla fenda é dada pela soma ponderada dessas duas ondas secundárias. Esta é a razão pela qual um conjunto de átomos produz franjas de interferência no anteparo de detecção: os máximos e mínimos de probabilidade refletem as diferentes relações de fase existentes entre as duas ondas 
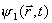
e 
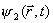
em pontos diferentes da tela de detecção (ver figura 1 e a discussão relacionada). Em analogia com o caso óptico, o espaçamento entre as franjas é proporcional ao comprimento de onda λ dos átomos. Isso explica porque a interferência não pode ser observada em um experimento de dupla-fenda com corpos macroscópicos. De fato, de acordo com as relações de de Broglie, o espaçamento inter-franjas se mostra extremamente pequeno para objetos com grande massa. Tão pequeno, de fato, que nenhum detector físico tem resolução suficiente para distinguir a interferência entre os máximos e os mínimos.
Em geral, entretanto, se um conjunto de sistemas mostra ou não interferência não é uma questão de tamanho. Na verdade, depende da quantidade de informação disponível em princípio ao observador. Para deixar este ponto mais claro, vamos voltar ao experimento da dupla-fenda e calcular a probabilidade p(x) de detectar um átomo em um ponto de coordenada x ao longo do eixo perpendicular ao feixe de átomos. Seguindo a abordagem de Richard Feynman, nós consideramos os dois ‘caminhos’ possíveis conectando a fonte de átomos a cada ponto da tela de detecção (ver figura 6). Nós vamos chamar os caminhos vindo da fenda 1 de: caminhos ‘↑’, e os caminhos vindo da fenda 2 de: caminhos ‘↓’.
Figure 6. Para cada ponto da tela de detecção é possível imaginar dois caminhos convergentes para o átomo, cada qual vindo de uma das fendas.
Nós também podemos associar um vetor de estado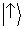
para os átomos seguindo o caminho ‘↑ ’: 
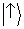
é o vetor de estado que prevê para a posição dos átomos na tela a distribuição observada em um aparato no qual somente a fenda 1 está aberta (curva vermelha da figura 4). Da mesma forma, nós chamamos de 
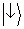
o vetor de estado que prevê a distribuição observada num aparato no qual somente a fenda 2 está aberta (curva azul da figura 4). Tendo estabelecido essas definições, nós podemos discernir dois casos.
• Caso 1 – CAMINHOS INDISTINGUÍVEIS
Suponha que não como saber se o átomo seguiu um caminho ‘↑’ ou um caminho ‘↓’ (os caminhos são ditos, nesse caso, serem indistinguíveis). O vetor de estado representando essa situação é o seguinte:
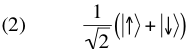
Aplicando a regra de Born ao estado (2), é possível derivar formalmente a distribuição espacial p(x) esperada neste caso. Nossa discussão prévia sobre funções de ondas nos dá a receita necessária para desenvolver esse cálculo simples. Nós obtemos:
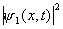
e 
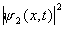
correspondem às distribuições vermelhas e azuis na figura 4 respectivamente. Além da soma ponderada desses dois termos (curva verde A na figura 4), a probabilidade associada com o estado (2) contém termos ‘cruzados’. É fácil de ver usando a eq. (1) que os termos cruzados oscilam como função de x. Quando somada ao primeiro e segundo termo, esta função oscilante dá origem ao típico padrão de interferência (curva verde B na figura 4). • Caso 2 – CAMINHOS DISTINGUÍVEIS
Vamos agora considerar o caso no qual é possível discriminar os caminhos (sem perturbar o movimento dos átomos). Suponha, por exemplo, que os átomos estão excitados e decaem emitindo um fóton exatamente enquanto passam pela fenda (figura 5). Detectar o fóton emitido permitiria trazer a informação ‘por qual fenda’ para o nosso conhecimento. Assim, os caminhos ‘↑’ e ‘↓’ agora são distinguíveis (no sentido de que eles podem – em princípio – ser distinguidos). Seja W o fóton observável carregando a informação ‘por qual fenda’, e vamos convencionalmente chamar de ‘
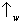
’ o resultado de W que indica a fenda 1 e ‘
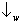
’ o resultado de W que indica a fenda 2. O vetor de estado correspondente à nova configuração experimental é o seguinte estado emaranhado, envolvendo o átomo e o fóton emitido: 
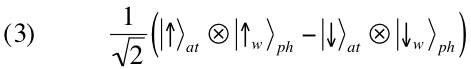
De acordo com a definição do estado emaranhado, se o fóton indica
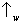
, então o átomo vai seguir a distribuição de probabilidade prevista pelo estado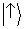 
, mas se o fóton indica 
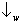
, então o átomo vai seguir a distribuição de probabilidade prevista por 
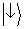
. Visto que cada fóton indica ou 
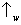
ou 
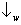
, fica claro que cada átomo é obrigado a seguir ou a distribuição espacial associada com 
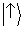ou a associada com 
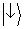
. Portanto, se olharmos para os átomos detectados ignorando a informação fornecida pelofóton, nós teremos uma distribuição espacial que é simplesmente a soma ponderada das distribuições de probabilidade previstas por 
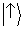
e 
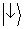
respectivamente. Os pesos das somas são as probabilidades dos resultados 
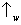
e 
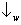
ocorrerem, sendo ½ e ½. 
Termos cruzados e, portanto, franjas de interferência, estão ausentes neste caso (compare com a discussão sobre os estados emaranhados de partículas de spin ½ ).
O desaparecimento da interferência quando a informação ‘de por qual fenda’ se torna, em princípio, disponível não deveria parecer tão surpreendente. Os vetores de estado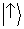
e 
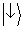
dos átomos podem ser expressos como sobreposições tanto de autoestados de posição ou autoestados de momentum. Portanto, eles atribuem probabilidades não somente para posições diferentes, mas também para diferentes momenta. Em particular, o estado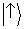 
atribui probabilidade 0 para os momenta indicando que ‘o átomo está vindo da fenda 2’, enquanto o oposto é verdadeiro para 
.
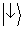
Assim , disponibilizando a informação ‘por qual fenda’ implica medir(parcialmente) o momentum do átomo. Como a posição e o momentum são observáveis incompatíveis, uma medição do momentum inevitavelmente modifica a distribuição espacial dos átomos na medição subsequente de posição. A interferência, em particular, é eliminada (ver a discussão dos estados quânticos para mais detalhes). As regras de Feynman são ferramentas poderosas que podem ser utilizadas em diversos contextos, desde que um conjunto de ‘caminhos’ e as correspondentes amplitudes de probabilidade tenham sido identificados. A Interferência por si só é uma característica geral dos fenômenos quânticos, não sendo limitada às medições de posição. Não importando como um sistema é preparado, é possível encontrar um observável tal que a distribuição de probabilidade associada com seus resultados mostre interferência (o que significa que alguns resultados são encontrados com alta probabilidade, enquanto outros nunca são encontrados). Em geral, se o estado do sistema pode ser escrito como uma sobreposição dos autoestados de um observável A, as franjas de interferência são observadas quando se está medindo um observável B incompatível com A. A condição para interferência ser observada é que não haja informação disponível de ‘por qual caminho’ (nem mesmo em princípio), i.e. que não exista nenhum observável C cujos resultados estejam correlacionados com aqueles do observável ‘caminho ’ A (ver o exemplo do observável de spin).
Os efeitos de interferência ilustram a conexão profunda entre o princípio de sobreposição, observáveis incompatíveis e complementaridade. Essa ligação mostra por sua vez até qual extensão o núcleo matemático da teoria quântica é determinado pelas relações existentes entre os observáveis que nós usamos para ‘estruturar’ os fenômenos físicos (ver implicações).