INCERTEZA > Origens As relações de incerteza expressam uma restrição estrutural que se aplica aos resultados estatísticos de medições envolvendo observáveis incompatíveis. Para ver o que significa dois observáveis serem incompatíveis, vamos considerar dois observáveis A e B separadamente. Um sistema sempre pode ser preparado (ao menos em princípio) de tal modo que ao se repetir diversas vezes a sequência ‘preparação P + medição de A’, sempre é possível obter o mesmo valor a_i. (Se diz nesse caso que, dada a preparação P, a probabilidade de encontrar a_i e A for medido é 1.) De modo análogo, é possível preparar um sistema de tal modo que a probabilidade de obter b_i em uma medição de B seja 1. Entretanto, se os dois observáveis forem incompatíveis, é impossível encontrar um procedimento de preparação tal que a medição conjunta de A e B resultará a_i e b_i com probabilidade 1. Em outras palavras, as medições de A e B parecem como se elas não fossem independentes (como se elas ‘interferissem’ entre si).

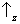
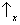
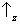
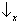
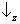
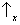
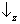
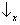
Este fato está ligado a relação geométrica existente entre as estruturas que representam observáveis incompatíveis no espaço de estados. Uma ilustração simples é dada pelo caso de duas componentes de spin S_z e S_x. Considere o modelo discutido na seção sobre o princípio de sobreposição. Fica claro que nenhum vetor de estado atribui probabilidade 1 a um dos seguintes resultados: & , & , & , & . (Isso é porque o eixo representando S_x e o eixo representando S_z no espaço dos estados não são nem paralelos nem ortogonais.)

Ao se generalizar esse tipo de argumento para o formalismo dos espaços de Hilbert, é possível provar que, já que posição e momentum são observáveis incompatíveis com um espectro de resultados contínuo, eles devem obedecer à desigualdade (1).

Devido a suas conexões profundas com a complementaridade, as relações de Heisenberg estão ligadas ao comportamento ondulatório dos sistemas quânticos. De fato, um teorema bem conhecido da análise de Fourieur que a largura espectral Δk de um sinal é inversamente proporcional à sua extensão espacial Δx. Se, de acordo com Louis de Broglie, nós associamos um pacote de onda de largura espectral Δk = hΔp/2π a uma partícula, a relação de Fourier para o pacote de onda dá exatamente (1).