SOBREPOSIÇÕES > Evidência

A mecânica clássica assume que a posição e o momentum de uma partícula têm um valor bem definido em qualquer instante. Se esses valores forem medidos, é possível calcular suas evoluções e prever o resultado exato de uma medida subsequente. Esse quadro determinístico é, entretanto, impreciso quando lidamos com observáveis incompatíveis. Como exemplo podemos considerar medições envolvendo componentes espaciais diferentes do spin. O spin é um observável de qualquer partícula quântica. Ele tem dimensões de momentum angular e faz parte de todos os processos envolvendo aquela quantidade física. Devido aos seus Spin, os elétrons reagem a um gradiente do campo magnético da mesma forma que uma carga elétrica faria. O spin é representado por um vetor. Entretanto, diferentemente do momentum angular ‘externo’ (i.e. o momentum angular associado com o movimento rotacional e translacional das partículas), cada componente de spin (S_x , S_y , S_z) só podem assumir valores discretos (que são múltiplos da constante de Planck h). Isso é facilmente visto em um experimento Stern-Gerlach com átomos de prata.

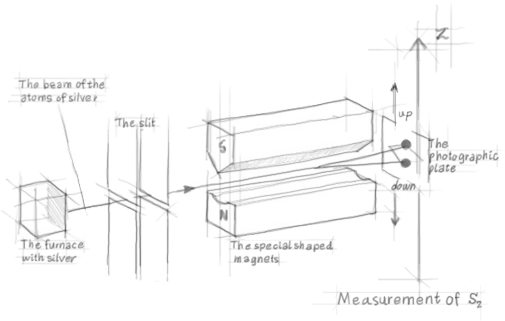
Figura 1. Experimento Stern-Gerlach.

Por cause de sua estrutura eletrônica, os átomos de prata têm um spin global que pode ser aproximadamente identificado com o spin do elétron orbitando a camada eletrônica exterior. Se um feixe de átomos de prata for direcionado através de um campo magnético não-homogêneo com gradiente vertical, ele se divide em duas componentes bem separadas ao longo do eixo z (ver figura 1). Esse é exatamente o comportamento esperado de dois conjuntos de átomos que possuem momenta angular igual em módulo mas apontando em sentidos distintos (como dois peões girando ou no sentido horário ou no anti-horário com a mesma velocidade angular).

A mesma divisão ao longo do eixo paralelo ao gradiente do campo magnético é observada se o experimento for repetido mudando a orientação dos imãs. Assim, o que nós encontramos é que a componente de spin ao longo de qualquer direção pode apenas assumir dois valores que nós convencionalmente chamamos de spin para cima e spin para baixo.

Figura 2. Seleção de Sz 'para cima'.

A incompatibilidade de duas componentes ortogonais do spin, por exemplo S_z e S_x, aparece quando nós tentamos preparar os átomos de tal modo que uma medição conjunta de S_z e S_x deveria nos dar para cima-para cima com probabilidade 1, i.e. p(S_z= ↑ & S_x= ↑ )=1. A figura 2 mostra que o processo de filtragem através do qual nós preparamos átomos para os quais p(S_z= ↑). Um filtro análogo (com os imãs orientados perpendicularmente) pode ser usado para preparar átomos para os quais p(S_x= ↑).

O problema é que se tentamos implementar um processo de dupla filtragem de modo a preparar átomos para os quais p(S_z= ↑ & S_x= ↑)=1 (figura 3), ele simplesmente não funciona! Quando saindo do filtro S_x, os átomos evidenciam S_z= ↑ ou S_z= ↓ com igual probabilidade (e não, como poderia se esperar em um modelo determinístico, S_z= ↑ com probabilidade 1).

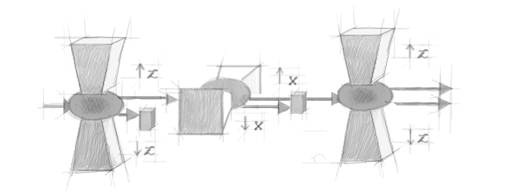
Figure 3. Duplo processo de filtragem.

Esse resultado indica que a probabilidade associada com os diferentes resultados em duas medições consecutivas de S_z é modificada de acordo com se S_x foi medido ou não entre as medições. É importante enfatizar que essa modificação ocorre independentemente da configuração utilizada para realizar a medição, i.e. isso não acontece por causa da natureza particular da interação entre os átomos e o aparato Stern-Gerlach. Ao invés disso, é uma característica típica das medições envolvendo dois observáveis que são mutuamente incompatíveis. Como mostramos na seção sobre origens, essa situação estranha pode ser facilmente representada por meio de vetores de estado dentro do espaço de estados.

O contraste entre modelos determinísticos (ver variáveis escondidas) e o formalismo quântico envolvendo observáveis incompatíveis se torna ainda mais agudo quando consideramos as correlações existentes entre pares de partículas emaranhadas. Experimentos com pares emaranhados (e também com trios e quartetos de partículas emaranhadas) têm sido realizados utilizando sistemas de dois níveis análogos às partículas com spin para-cima/spin para-baixo.

A polarização de fótons serve, por exemplo, como um análogo bem próximo ao spin do elétron. Caso se direcione um feixe de luz através de filtros polarizadores (que têm o papel do aparato Stern-Gerlach), os resultados observados são equivalentes àqueles descritos nesta seção. O eletromagnetismo clássico pode dar conta das observações nesse caso. Entretanto, quando os mesmos experimentos ópticos são realizados com fótons individuais, um tratamento quântico que faz uso essencial dos vetores de estado se torna necessário (ver também interferência de partícula).

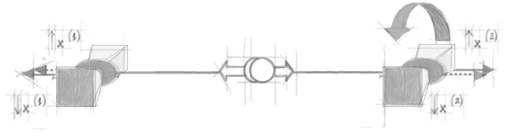
Figura 4. As correlações entre os spins de duas partículas emaranhadas são medidas por meio de dois aparatos Stern-Gerlach distantes. A orientação relativa dos dois aparatos pode ser mudada. Quando são paralelas, os spins das duas partículas são sempre encontrados apontando para sentidos diferentes (ver 'origens' para mais discussão).