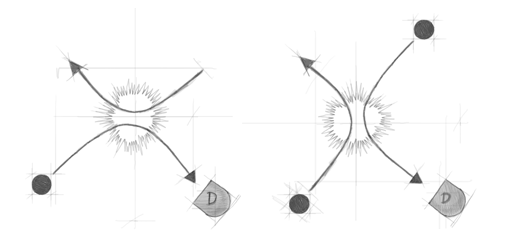
Figure 2. The two indistinguishable 'paths' that correspond to a given detection result in a scattering experiment with identical particles.
The effects of indiscernibility can be observed in scattering experiments. Let us consider an elastic collision between a helium nucleus (also called an α-particle) and an oxygen nucleus. We look at the collision in the center-of-mass frame, in which the particles have antiparallel velocities both before and after the collision. Suppose that a particle detector D is placed on an axis perpendicular to the initial trajectory of the particles. We first measure the rate Fα of α-particles scattered into D for a large number of collisions. Then we repeat the experiment, but this time we measure the rate FOXY of oxygen nuclei scattered into D. When we compare the results thus obtained, we find that FOXY = Fα. This is easily understood taking into account the fact that for each oxygen nucleus scattered into D, an α-particle is scattered in the opposite direction. However, for symmetry reasons, we expect the rate of α-particle scattered along any direction perpendicular to the initial trajectory, to be the same. Hence, the rate of α-particles scattered into D must equal the rate of α-particle scattered in the opposite direction. Hence Fα = FOXY. The total rate of particles counted by D (disregarding whether they are helium or oxygen) is therefore FTOT = Fα+ FOXY = 2Fα. We can repeat the experiment by changing the target particle (for example by replacing oxygen by carbon or beryllium): we always get FTOT = 2Fα . But now suppose that the target particles are themselves α-particles. In this case, we find FTOT = 4Fα. In other words, FTOT is increased by a factor 2!It must be stressed that this result has nothing to do with some special feature of helium. What really matters is the indiscernibility of the targets and the projectiles. In fact, if instead of using the same helium isotope for both the projectile and the target, we use for example 4He projectiles and 3He targets, the enhancement of FTOT is not observed. The projectile (4He) and the target (3He) are now distinguishable (by the number of their neutrons), so we recover the result found with oxygen.
An explanation of this phenomenon is provided by the indiscernibility principle. When the colliding particles are indiscernible, there are two indistinguishable paths leading to the detection of one particle in D (see Figure 1). Like in the double-slit experiment, the probability amplitudes corresponding to these two indiscernible possibilities interfere.
α-particles are bosons. What now if we repeat the experiment with two identical fermions, for example with two electrons with parallel spin? The result is amazing. As in the case of bosons, the value of FTOT is different from what is expected for distinguishable particles. This time, however, FTOT = 0. In other words, no perpendicular scattering is observed.