
Eq. (1) describes the temporal evolution of the compound system cat + atom. The atom is initially excited, which means that one of its electrons absorbed some energy and jumped into an outer atomic shell. As the probability of finding the atom still excited decreases, the cat-atom quantum state evolves into an entangled state (right-hand side of eq. (1)). At this stage, the atom and the cat are strongly correlated. For example, if the atom is found to be excited, we know for sure that, if we look at the cat, we will find it 'alive'. Conversely, if the atom is found to have decayed, the probability to find the cat 'dead' is 1. These perfect correlations have nothing extravagant. But they are only a small subset of the correlations implied by state (1). We have so far considered only one observable of the atom, namely its internal energy E, whose eigenvectors are
Let's consider now a different observable, Q, whose eigenvectors are the states:
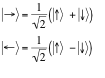
The physical meaning of such an observable can be understood in the framework of electromagnetism. However, for our purposes, it is sufficient to identify Q's possible outcomes, ' ←' and '→', with the mutually exclusive results of an experimental protocol that can consistently be called 'a measurement of Q'. (A helpful analogy is provided by spin observables: the relation existing between E and Q, as well as the relation existing between their respective eigenvectors, is similar to that existing between Sz and Sx, and between their respective eigenvectors.) Suppose we want to rewrite state (1) in terms of the eigenvectors of Q. In analogy with the case of two entangled spins, we get the following expression:

Having carried out these formal manipulations, we are now in a position to look at the consequences of Schrödinger's paradox. For, what happens to the cat if we measure Q on the atom and find for example '→'? It follows from eq. (2) and from the properties of entangled states that, in this case, the results of any further measurement performed upon the cat alone are those predicted by the following state vector:
Does this quantum state imply the existence of a cat which is simultaneously dead and alive? Not at all. If the biological state of the cat is tested, according to state (3) the cat is found to be alive half of the times and dead the other half. However, state (3) also predicts interference effects if the appropriate observable is measured. If these interference effects were usually observed, as they are for atoms (see wave-particle duality), our very concept of cat would be quite inadequate to deal with ordinary experience. As inadequate as the classical concept of particle is when it comes to microscopic phenomena (see uncertainty and wave-particle duality).
To explain why cat interference is not observed in ordinary experience, one must take into account the fact that real cats, like most macroscopic systems, are not isolated from their environment. For example, the atoms that compose a cat spontaneously emit photons which carry information about the emitting source. This and similar processes result in correlations between the cat and the environment which are described by an entangled state. By generalizing the argument outlined in the discussion of the double-slit experiment, one can see that, under these conditions, quantum mechanics correctly predicts that interference will not be observed.