UNCERTAINTY > Origins The uncertainty relations express a structural constraint that applies to the statistical results of measurements involving incompatible observables. To see what it means for two observables to be incompatible, let us first consider two observables A and B separately. A system can always be prepared (at least in principle) in such a way that by repeating several times the sequence ‘preparation P + measurement of A’, one always gets the same value a_i. (One says in this case that, given the preparation P, the probability of finding a_i if A is measured is 1.) Analogously, one can prepare a system in such a way that the probability of getting b_i in a measurement of B is 1. However, if the two observables are incompatible, it is impossible to find a preparation procedure such that a joint measurement of A and B will yield a_i and b_i with probability 1. In other words, the measurements of A and B look as if they were not independent (as if they ‘interfered’ with each other).

This fact is linked to the geometrical relation existing between the structures that represent incompatible observables in the state space. A simple illustration is provided by the case of two spin components S_z and S_x. Consider the toy model discussed in the section on the superposition principle. It is clear that no state vector assigns probability 1 to one of the following results: & , & , & , & . 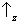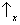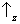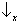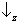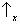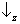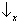(This is because the axis representing S_x and the axis representing S_z in the state space are neither parallel nor orthogonal.)

By generalizing this kind of argument to the formalism of Hilbert spaces, one can prove that, since position and momentum are incompatible observables with a continuous spectrum of outcomes, they must obey inequality (1).

Owing to their deep connection with complementarity, the Heisenberg relations are linked to the wavelike behaviour of quantum systems. In fact, it is a well-known theorem from Fourier analysis that the spectral width Δk of a signal is inversely proportional to its spatial extension Δx. If, following Louis de Broglie, we associate a wave packet of spectral width Δk = hΔp/2π with a particle, the Fourier relation for the wave packet reads exactly as (1).